Picking An Optimal Fantasy Team ⚽

Intro

Football, by which I mean the sport where you kick a ball with your feet, is quite dear to me. I used to play once or twice a week with friends and coworkers until my back couldn’t take it anymore. Those football sessions were often the highlight of my week, so I was quite reluctant to give it up.

Nowadays, I have to be content with watching football on TV, in particular the English Premier League. I also play a game called Fantasy Premier League. That gives me an added incentive to watch and track results of games that I wouldn’t otherwise bother with. I want to know how my players are doing. I also want to know how the players who I haven’t picked are doing and pray that they have a stinker of a game.

The first time I signed up to play I was asked to pick a squad of 15 players and was given a budget of £100 million to do so. I soon realized that this was an optimization problem.

Dynamic Programming

I learned about Dynamic Programming during an undergraduate course on the design and analysis of algorithms. Dynamic programming is an algorithmic paradigm in which a rather neat trick is used to efficiently find a solution in very large solution spaces. The trick is to break a large problem into a sequence of smaller, overlapping subproblems and remembering their solutions to prevent repetitive calculations. Not every problem can be divided up in such a way, but those that can be are solvable in polynomial or pseudo-polynomial time thanks to Dynamic Programming. We’ll take a look at three such problems in a bit.

Top-down vs Bottom-up

There are essentially two ways to implement a Dynamic Programming algorithm:

1. Top-down, using recursion and memoization.
2. Bottom-up, populating a table one element at a time.

The former is easier to reason about whereas the latter can be more performant. We’ll stick with top-down implementations throughout this article as premature optimization is the root of all evil. Rest assured that you can always transform a top-down implementation into a bottom-up one, should you need to.

Longest common subsequence (LCS)

Have you ever wondered how a diff is generated? It boils down to finding the longest common subsequence (LCS) of the two files. Whatever remains is the diff. Finding the LCS is solvable in quadratic time with Dynamic Programming. Here is a Python implementation, which you’ll notice is quite concise.

from functools import cache
 
@cache
def lcs(a: str, b: str) -> str:
    if len(a) == 0 or len(b) == 0:
        return ""
    if a[0] == b[0]:
        return a[0] + lcs(a[1:], b[1:])
    result_a = lcs(a[1:], b)
    result_b = lcs(a, b[1:])
    return result_a if len(result_a) > len(result_b) else result_b
 
# Example
# In:  lcs("Dynamic Programming Rocks", "Dynamic Functions Need Socks")
# Out: "Dynamic on ocks"

This implementation considers three scenarios:

1. The end of one or both strings has been reached
2. First letters are equal
3. First letters are different

Only the last scenario requires consideration of two different options, namely from which string to omit the first character. A naïve implementation would wander into exponential run-times here. A comparison of strings only 20 characters in length would take ages if it weren’t for the @cache decorator. It keeps track of (memoizes) previously computed results and returns those immediately.

The knapsack problem

Imagine that you’re going on a long and challenging hike. You have already packed the essentials for the hike. All that remains is to pack food. You bring out an assortment of items from your pantry. You want to bring as much energy in terms of calories as you can but there’s a limited amount of space left in your backpack (aka knapsack).

Our food items have two attributes that we care about:

• Utility, which in our case is caloric content
• Cost, which in our case is volume

The remaining volume in the backpack defines our budget, which constrains the set of items we can pick. Finding the set of items that fits in the bag with the most amount of calories is essentially the knapsack problem.

A brute-force search for the optimal set of items would involve trying out every possible subset of the n items. There are $2^n$ such subsets so that would only be reasonable for very small values of $n$.

Luckily, the knapsack problem can be solved with Dynamic Programming in $O(nB)$ time, where $B$ denotes the budget. The solution method is deceptively simple. We order the items arbitrarily, then consider each item in turn, for which we have two options.

1. Include the item in our set, subtract its cost from the remaining budget and then calculate the optimal set from the items that come after it.
2. Omit the item from the set, then calculate the optimal set from the items that come after it with the budget intact.

Whichever option that yields more overall utility is the one we choose. Here’s a Python implementation of this algorithm.

from dataclasses import dataclass
from functools import cache
 
 
@dataclass
class Item:
    utility: float
    cost: int
 
 
def knapsack(items: list[Item], budget: int) -> tuple[float, list[Item]]:
    @cache
    def pack(budget: int, index: int) -> tuple[float, list[Item]]:
        if index >= len(items) or budget <= 0:
            return 0, []
 
        # Option A, take item if budget allows
        utility_a, items_a = (0, [])
        current_item = items[index]
        if current_item.cost <= budget:
            utility_rest, items_rest = pack(budget - current_item.cost, index + 1)
            utility_a = current_item.utility + utility_rest
            items_a = [current_item] + items_rest
        
        # Option B, don't take item
        utility_b, items_b = pack(budget, index + 1)
 
        # Pick the best option
        return (utility_a, items_a) if utility_a > utility_b else (utility_b, items_b)
 
    return pack(budget, 0)

While not as simple as the LCS algorithm, it’s still pretty concise. Here we use a nested function so that we can pinpoint the two variables that should form the cache-key, namely the remaining budget and the position within the items list from which to start the search.

There are many variations of the knapsack problem. Some are simpler, others more complicated. For practical applications, it’s not unusual to have to account for more dimensions for utility and/or cost. For example, we may want to consider both the volume and weight of an item. As we will see, picking an FPL team requires that we consider several constraints.

Fantasy Premier League (FPL)

At the start of a new Premier League season, fantasy managers are given a budget of 100 million pounds. That may not seem like a lot given that PSG paid £198 million for Neymar. However, player prices in FPL are a lot more modest, ranging from £4 to £15 million (which buys you a tall Norwegian sporting a pony-tail).

Beyond the budget, FPL imposes two additional constraints:

• The squad must consists of 2 goalkeepers, 5 defenders, 5 midfielders and 3 forwards for a total of 15 players.
• At most 3 players can be picked from the same club.

In the knapsack algorithm, we used the (budget, index) tuple to form our cache key. To handle the additional constraints, we need to add more elements to it. For the squad makeup, we introduce variables that track how many slots are still available in a given position. The cache key therefore becomes

(budget, index, goalies_left, defenders_left, midfielders_left, forwards_left)

The club constraint is trickier since there are 20 clubs in the Premier League. We could add one element per club to keep track of our 3-players budget. That would however increase the dimensionality of our search space from 6 to 26. Each of those 20 additional dimensions has 4 possible values (0, 1, 2 and 3) so the algorithm might take up to $4^{20}$ times longer to run. In case you’re wondering, $4^{20}$ is approximately 1.1 trillion.

For the sake of efficiency, we take a shortcut. In my experience, it’s sufficient to enforce the 3-player constraint for a single dominant club so we just add one more element to the cache key. The complete implementation of this algorithm can be viewed here.

Tactical matters

Player utility

The utility of FPL players equals the amount of points we believe they’ll accrue per match. This sounds simple but isn’t. The outcome of matches is difficult to predict and the performance of individual players doubly so. Anyone who has managed an FPL team for a season or two probably has stories of gameweeks gone horribly wrong. Players might suddenly be benched, get injured or fall ill. Others might play but get sent off, score an own goal or miss a penalty. A transfer might backfire catastrophically, with the transferred-out player having a fantastic gameweek following a disappointing run.

That being said, performances tend to even out over a longer term. When picking a squad at the beginning of a season, one might look at how many points a player received during the previous season, or perhaps the latter half of the previous season. This conservative strategy will yield a squad of veterans, players who have proved their mettle in FPL. It will, however, overlook players of promoted teams and players who were transferred in from other leagues over the summer.

It’s easier to predict player performance once the season is well underway. In FPL, managers are given two opportunities to overhaul their squad completely using a so-called wildcard chip. In the code that I’ve supplied, the utility of a player is estimated to be the same as their points-per-match in previous gameweeks this season. This is a very simple estimator but it’s a good starting point. A better estimator would consider recent form and the difficulty of upcoming matches. An even better one would take into account how much of an impact match difficulty has on the performance of the individual player. The code is easy to extend should you want to implement your own utility function.

Substitutes

In FPL, 11 players form a team while the remaining 4 are substitutes. The points of the substitute players only count if one or more team players don’t play a single minute during the current gameweek. Hence, most of the points that the substitutes gather over the season won’t count towards the points of your team. The algorithm optimizes for overall utility but the utility of the substitutes is mostly wasted. I would therefore suggest to hand-pick 3-4 substitutes rather than have the algorithm pick them. An ideal substitute is one that is dirt cheap but is still a regular starter for their team.

The captain

The player with the captain’s armband scores double points. The algorithm doesn’t take this into account when picking a squad with the most overall utility. For that reason, you may want to hand-pick the player who you intend to be your captain.

Example

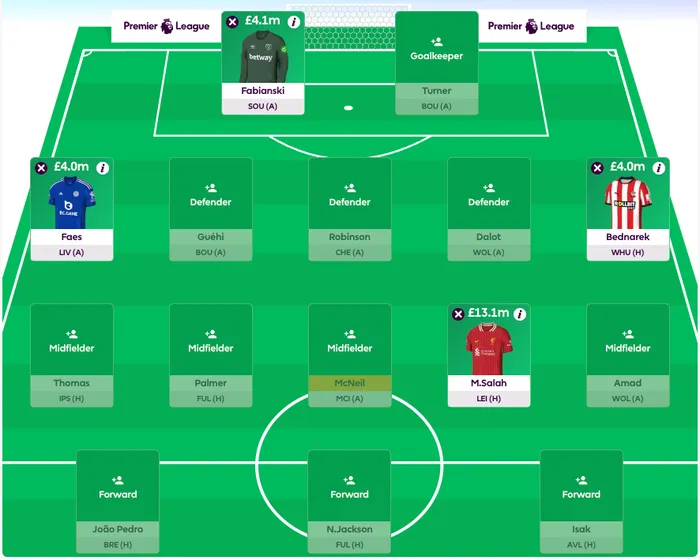
Here’s a squad containing 3 cheap substitutes and Mo Salah who will be our captain. We update the constraints for the selection, adjusting the empty positions and remaining budget. We also add Mo Salah’s id (328) to the ignore-list because we’ve already picked him.

# The number of positions to fill. Lower these if you've already picked players for your bench
# and/or that one player you plan to captain every week.
# The order is [goalkeepers, defenders, midfielders, forwards]
empty_positions = [1, 3, 4, 3]
 
# Players that you want to exclude from the selection. For example, if you've already picked Haaland
# and just want to fill up the rest of the team, then put his id in this list.
# To find a player's id, consult data/player_data.json
# Examples based on ids from the 24/25 season
#  - [351] to exclude Haaland
#  - [328] to exclude Salah
#  - [328, 351] to exclude Salah and Haaland
ignored_player_ids = [328]
 
# Your remaining budget in £ millions
budget = 74.8

We then run the algorithm which, after a few seconds, produces the following results:

> python a02_pick_squad.py
Picking squad from a pool of 279 players. This will take some time...
  id  name                            cost    points    form    utility    team_nr  position
----  ----------------------------  ------  --------  ------  ---------  ---------  ----------
 310  Alisson Ramses Becker            5.4        36     0.2        5.1         12  gk
 422  Ola Aina                         4.9        75     4.5        4.4         16  def
 238  Ashley Young                     4.7        62     5.6        4.8          8  def
   3  Gabriel dos Santos Magalhães     6.2        73     4.7        4.9          1  def
 494  James Maddison                   7.6        91     6.5        5.7         18  mid
 364  Amad Diallo                      5.3        65     6.3        4.6         14  mid
 182  Cole Palmer                     11.2       128     7.3        8            6  mid
  99  Bryan Mbeumo                     7.6       107     5.2        6.3          4  mid
 447  Chris Wood                       6.6        92     4          5.4         16  fwd
 401  Alexander Isak                   8.9        97     8.3        6.5         15  fwd
 110  Yoane Wissa                      6.3        76     3.7        5.4          4  fwd

That’s a solid squad that should draw envious glares from other FPL managers. While there are no guarantees that these players will continue to perform as well as they have, this selection provides a nice foundation upon which to build a competitive FPL team.

Where to get the code

Feel like giving it a go yourself? Head on over to my GitHub Repository. Refer to the README for instructions on how to run and tweak the code.